What will be

Here, as we go on adding infinite terms will the sum of the series go on increasing to infinity or will it get closer and converge to some finite number?

Before calculating the sum of the above series using the analytical method let me show you a geometric method of arriving at the result.

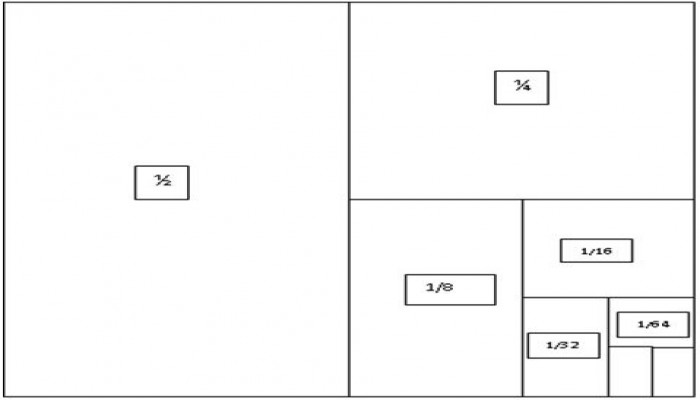
Refer Figure 1.

Figure 1

Let us consider a unit square. The area of this square is 1 square units. Let us divide this square into a half as shown in the figure. The area of each part will be ½ square units. Now, let us divide one of these parts into its half as shown in the figure. The area of each of these parts will be ¼ square units. Now, let us divide one of these parts into its half as shown in the figure. The area of each of these parts will be 1/8 square units. Now, go on repeating the process as shown in the figure.

 

Now, let us add the areas of all these parts, we get:

This is what we began with.

From the above figure, we observe that as we go on adding areas of more parts the sum gets closer to 1. We also observe that the sum will not be greater than 1. In other words 1 is the limiting value of the sum of the infinite series.

Hence, we have

The terms of the given infinite series are in geometric progression. That is, the consecutive terms of the series are having a constant ratio. ½ in this case.

Let

be an infinite geometric series with common ratio r. Then, we have

If, r < 1 then the sum s will converge to a finite value.

In the given series we have r = ½. Hence, it is convergent. Hence, we have

Hence, we have

Now, let us look at the sum of one more infinite geometric series:

Here, r = ¼, hence we have

You might be wondering who must have been the first mathematician to calculate the sum of this infinite geometric series?

It was Virasena who had done so in his commentary Dhavala (816 CE) on the Digambara Jain text Satkhandagama. He had calculated the sum of this infinite series to evaluate the volume of the frustum of a right circular cone.

This summation was proved by Nilakantha Somayaji (1444-1544 CE) (mathematician from Kerala in south India) in Aryabhatiyabhasya his commentary on Aryabhatiya. He states that:

चतुरंशपरम्परासमुदायः कृत्स्नोऽपि त्र्यंश्त्वमेवापाद्यते।

कथं पुनः तावदेव वर्धते तावद्वर्धते च​?

The entire series of powers of ¼ adds up to just 1/3. How is it that the sum of the series increases up to that limiting value and that it actually does increase up to that limiting value?

Nilakantha Somayaji then goes on to prove the result of the summation. He started with

Let us add up all the above equations. We get:

Nilakantha Somayaji then presents the following argument to derive the sum of the infinite geometric series:

As we go on adding more terms, the difference between 1/3 and the sum of powers of ¼, becomes extremely small, but never zero. Only when we add infinite terms do we obtain the equality:

This was a significant development on the path of development of calculus in India by the mathematicians from the Kerala School of mathematics. For more on this visit:

https://www.manchester.ac.uk/discover/news/indians-predated-newton-discovery-by-250-years/

Image provided by the author.