Should a tolerant person tolerate intolerance? At an individual level this is a paradoxical question. How a person intolerant of intolerance could be called, by definition, tolerant? This is a pertinent dilemma for an idealist mind. Idealism insists on consistency, and it does not allow one's moral code to be influenced by others' behavior.

We evolved to live in society because all other things being equal, one living in society finds survival easier than a solitary individual. But social living came with the burden of tolerance, cooperation, and altruism. A society is better off if its members are altruistic and cooperative. However, being altruistic and cooperative is disadvantageous to the individual interest. Game theory studies mathematical model of conflict and cooperation between rational decision-makers. In game theory, a common model of social cooperation is Prisoner's dilemma. Here a group of players would collectively be better off if they could play Cooperate, but since Defect fares better individually, player has an incentive to play Defect.

The prisoner's dilemma:

Two partners, caught committing a minor crime, are suspected by police to have committed a much serious crime. Both are held in solitary confinement so they have no means to communicate with each other. Both are separately offered a bargain to testify against each other.

Here are possible scenarios:

1. If both remain silent, each will serve 1 year in prison for the minor crime.
2. If one betrays while the other remains silent, the betrayer will go free but the one who remained silent will serve 5 years in prison.
3. If both betray then each will serve 3 years in prison.

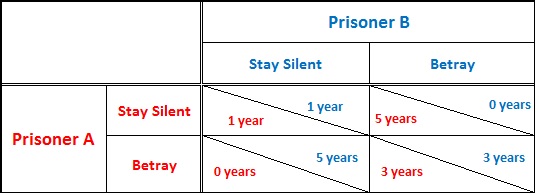
If both remained silent, each will face imprisonment for only 1 year – this is the best proposition for the group; however, fear of being deceived and getting penalized 5 years prison for trusting the partner is likely to convince both of them to defect.

Next, if the game is played repeatedly between the same players, a player can have flexible strategy to cooperate or defect based on the previous actions of the opponent. This extended version is called iterated prisoner's dilemma. Multi-player version of the game can model transactions between two people requiring trust, cooperative behavior in society. This assumption has made the iterated prisoner's dilemma game fundamental to some theories of human cooperation and trust. Does it make sense then to continue cooperating if the opponent never cooperates? Does such blind strategy encourage exploitation by predatory strategies?

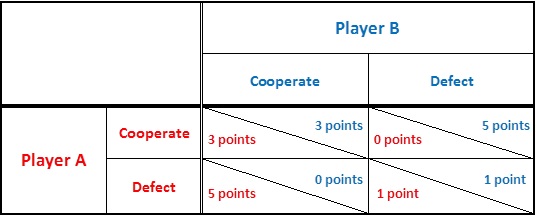
What will happen if a player AC (Always Cooperate) plays against a player NC (Never Cooperate, or Always Defect)? After each move, AC will gain 0 points, but NC will gain 5 points. If the game is played repeatedly, in all encounters AC will never benefit because of his blind optimist strategy while NC with his negative strategy will benefit handsomely.

What kind of strategies can encourage cooperation without falling victim to the exploitative strategies? To seek the answer, Robert Axelrod, a political scientist, organized a computer tournament in 1980. He invited well-known game theorists, psychologists, sociologists, political scientists, and economists to submit their computer program for the iterated prisoner's dilemma. The challenge offered was straightforward: The tournament was structured as round-robin meaning each entry was matched against each entry submitted. A program could record the history of the matches played, and use it to devise the strategy. The highest scoring strategy was to be the winner.

The first round of the tournament had 14 contestants. The winning strategy -"TIT FOR TAT" was relatively simple: Cooperate when facing an opponent first time; subsequently do what the opponent did in the previous move. It means cooperate if last time opponent cooperated, defect if last time opponent defected. Results of a single tournament are not considered definitive; therefore second round of the tournament was conducted. It had 62 contestants. Second round participants knew the first round results. They were also aware of the approaches adopted by successful entries in the first round. Nevertheless, the winning strategy was again "TIT FOR TAT".

By analyzing the top-scoring strategies, Axelrod found several conditions necessary for a strategy to be successful.

• Nice: The most important condition is that the strategy must be "nice", that is, it will not defect before its opponent does (this is sometimes referred to as an "optimistic" algorithm).
• Retaliating: However, the successful strategy must not be a blind optimist. It must sometimes retaliate. An example of a non-retaliating strategy is Always Cooperate. This is a very bad choice, as "nasty" strategies will ruthlessly exploit such players.
• Forgiving: Successful strategies must also be forgiving. Though players will retaliate, they will once again fall back to cooperating if the opponent does not continue to defect.
• Non-envious: The last quality is being non-envious, that is not striving to score more than the opponent.

Now, imagine that each computer program from the tournament is transformed into a distinct animal species. Each species receives one game strategy as an inheritable behavioral trait. They remember history of their past interactions, and the inherited strategy decides if they should cooperate or defect. A round of tournament becomes equivalent to one generation of the species; and in proportion to their score, they multiply or decline. Obviously, the next generation offspring will inherit the same strategy, making them behave identically to their parent. Suppose one or more species of animals are cloned to an initial population and left on an island, what will follow is close to an evolutionary process. Evolutionary game theory (EGT) is the application of game theory to evolving populations. After a few generations, some species will thrive while other will decline. EGT helps us to identify if there is any evolutionarily stable strategy among the group. An evolutionarily stable strategy (ESS) is a strategy which, if adopted by a population in a given environment, cannot be invaded by any alternative strategy that is initially rare.

Let's see if populations of AC (Always Cooperate), NC (Never Cooperate), and TFT (TIT for TAT) are put together and allowed to evolve, what happens.

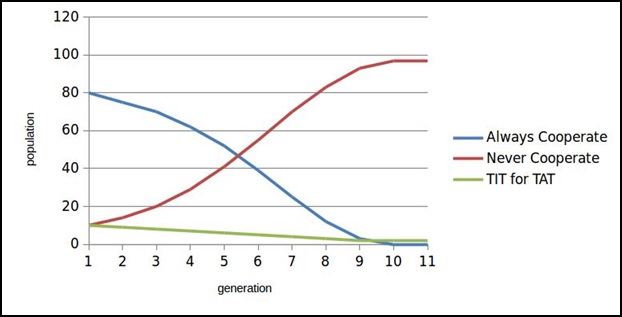
In AC dominant population, an invasion of a small group of NC will prove fatal. AC population will be eliminated after a few generations, and NC will gain dominance. Presence of small TFT population has no significant effect.

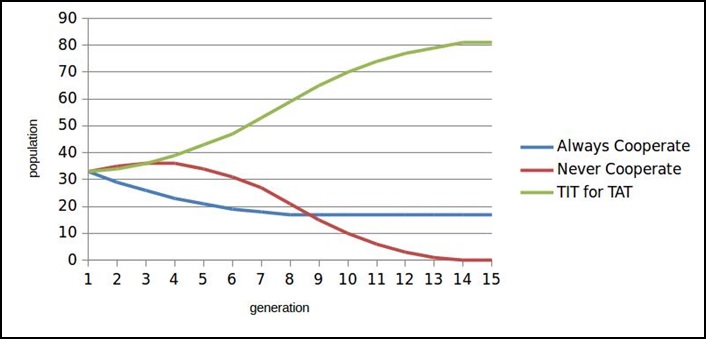
When AC, NC, and TFT populations are present in equal proportion, NC will get eliminated after a few generations. AC population will decline initially, but it will be able to survive along with thriving TFT population.

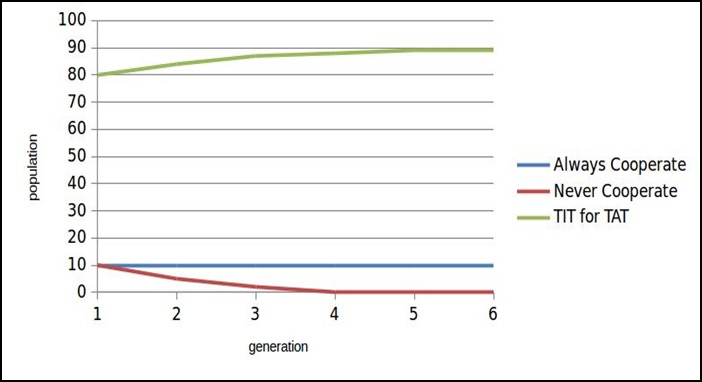
If large population of TFT exists, invasion of a small group of NC will prove futile. Coexisting AC population will be able to live without being harmed while NC will get eliminated.

Some conclusions from the study are self-evident: Blindly optimistic strategy Always-Cooperate is not an ESS. It will decline and disappear in the presence of a negative strategy Never-Cooperate. In contrast, Tit-for-tat is an ESS. Since it supports cooperation without being gullible, Tit-for-tat can coexist with Always-Cooperate, but an invasion of Never-Cooperate will put selective pressure against Always-Cooperate, and in favor of Tit-for-tat.

Game theory is an abstraction, and like any abstraction, it cannot be applied to the real world in its pure form. The perspective it offers on tolerance of intolerance, however, reflects what philosopher Karl Popper had to say on the paradox of tolerance in 1945:

"Less well known is the paradox of tolerance: Unlimited tolerance must lead to the disappearance of tolerance. If we extend unlimited tolerance even to those who are intolerant, if we are not prepared to defend a tolerant society against the onslaught of the intolerant, then the tolerant will be destroyed, and tolerance with them."

References:

1. Robert Axelrod, "The Evolution Of Cooperation"
2. William Poundstone, "Prisoner's Dilemma"
3. https://en.wikipedia.org/wiki/Game_theory
4. https://en.wikipedia.org/wiki/Evolutionary_game_theory
5. https://en.wikipedia.org/wiki/Evolutionarily_stable_strategy
6. https://en.wikipedia.org/wiki/Prisoner's_dilemma
7. https://en.wikipedia.org/wiki/Paradox_of_tolerance
8. http://www.lifl.fr/IPD/ipd.frame.html